AI特許について理解する前提としてAI自体を理解する必要があります。AIの一態様に機械学習があります。機械学習には、「教師あり学習」、「半教師あり学習」、「教師なし学習」、「強化学習」などがあります。
AIの基礎 機械学習 教師あり学習
教師あり学習は、学習データとそのデータの正解データとの組み合わせをコンピュータに与え、徳地陽、ルールを学習させる方法で、分類問題、回帰問題などに利用されます。
たとえば、学習データとして猫の画像がある場合に、その猫の画像の正解データとして猫の文字列を付与されます。このような正解データは人間によって付与されます。
AIの基礎 機械学習 教師あり学習 分類問題

分類問題では、たとえば、迷惑メールと思われる文字列(たとえば、儲かるなど)に重みづけをしてマイナス点を与え、普通のメールと思われる文字列(たとえば、お世話になっております)に重みづけをしてプラス点を与え、合計点数が閾値未満であればスパム・メールと判断するものがあります。
AIの基礎 機械学習 教師あり学習 回帰問題
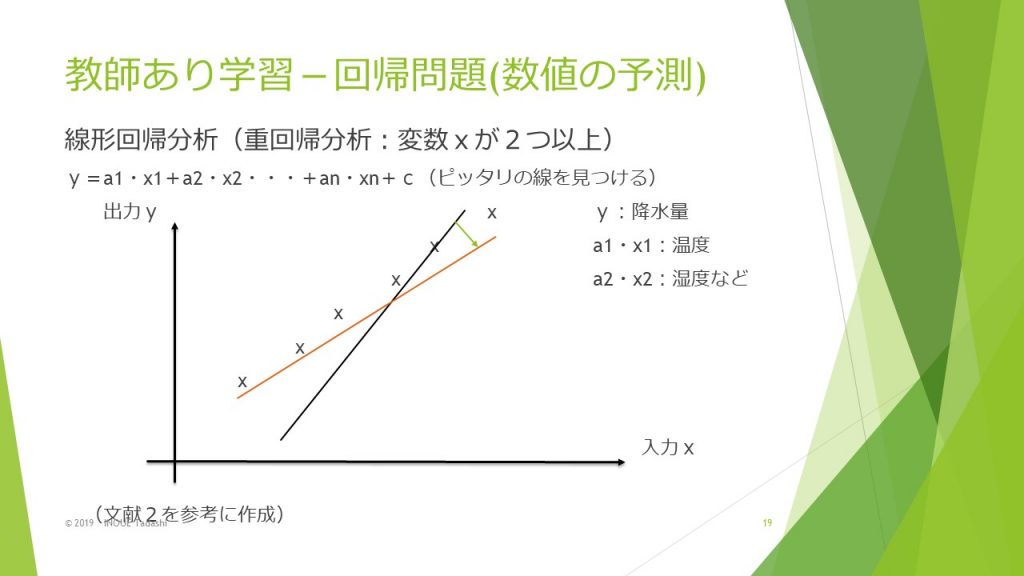
回帰問題では、データの分布に適したラインを考えるという線形回帰があります。上記の重回帰分析では入力が温度と湿度との2つあり、出力が降水量となっています。このような分布から最適なラインを見つけ出し、温度と湿度との2つの入力があった場合に、降水量を予測するものです。
上記の例では変数が2つのため重回帰分析ですが、変数が1つであれば単回帰分析となり、出力yを変数xのn次多項式で表す多項式回帰分析というものもあります。
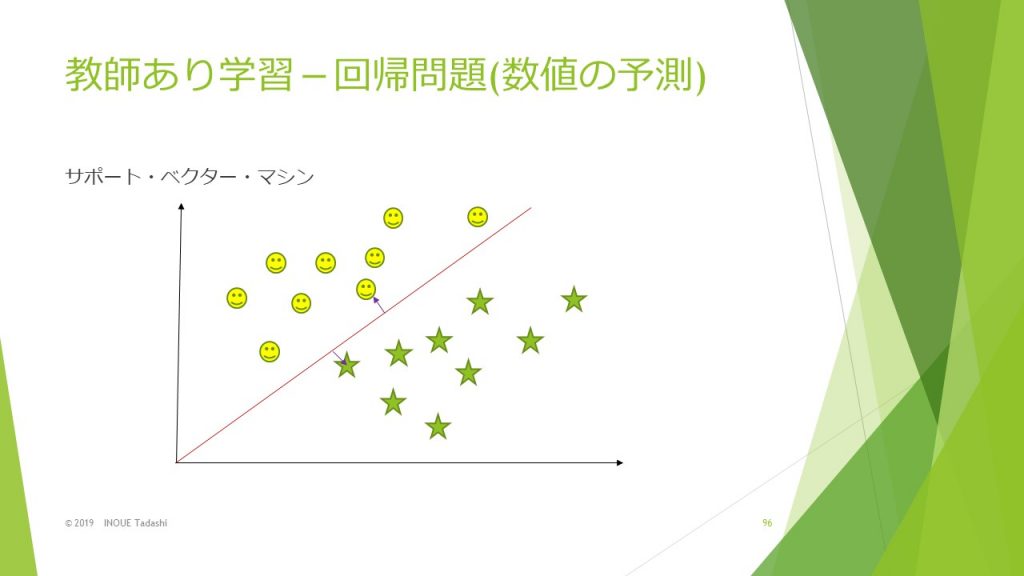
サポート・ベクター・マシンは、データとの距離が最大となるような境界線を求めることで、データの分類を行うものです。
境界線とデータとの距離をマージンといい、境界と最も近くにあるデータをサポート・ベクトルといいます。
また、シグモイド関数などを利用するロジスティック回帰というものもあまります。ロジスティック回帰は「回帰」という名前がついていますが、分類問題に利用されます。
AIの基礎 機械学習 教師なし学習

教師なし学習は教師あり学習と異なり、正解データが無い状態で入力データの変換、分類を行う機械学習です。
k-means法は、教師なし学習の代表的な手法でデータのクラスタリングによく用いられます。
n次元の空間上にデータを分布させ、最初はランダムにk個のクラスに分類します。それぞれのクラスのそれぞれの重心を算出し、算出した重心に近いデータごとに改めてクラスに分類します。さらに、改めて分類されたクラスのそれぞれの重心を再度算出し、再度算出された純真に近いデータごとに改めてクラスに分類します。このようにクラスの分類と重心の算出とを繰り返すことにより最終的に集束したk個のクラスに分類されます。
但し、k-means法において注意しなければならないのは、k個に分類されますが、k個に分類されたデータの特徴は人間が判断するということです。つまり、なんだかわからないけれどk個のクラスには分類できる、ということです。その分類されたk個のクラスに含まれているそれぞれのデータをみて、「これは猫の画像のグループ」、「これは犬の画像のグループ」というように判断するのは人間です。
主成分分析は、次元削減の代表的な手法です。
主成分分析では、多くのデータの集まりであるデータ群が存在した場合にそのデータ群の大まかな特徴がわかります。たとえば、データ群のデータを二次元空間に分布された場合に、そのデータの分布の多い傾きの直線を引くことにより、その直線はデータ群の大まかな特徴を表すこととなります。たとえば、データ群の特徴を10割表すことはできないけれど、7割程度の特徴を表すということになります。
AIの基礎 機械学習 半教師あり学習

半教師あり学習は、少量の教師データを用いて簡単に学習させるものです。
AIの基礎 機械学習 強化学習

強化学習は試行錯誤を通じて価値を最大化するものです。
ランダムに動いて報酬または罰と行動とのペアを記憶し、報酬をもらえそうな行動を行い、報酬がもらえたら、その報酬と行動とのペアを強化します。
探索と活用とは完全に分けて行うA/Bテスト、探索と活用とをミックスしながら行うバンディットアルゴリズムなどがあります。
(弁理士 井上 正)



